WebGL ( 6 - Martrix )

이번에는 3D를 표현하기에 앞서
Matrix(행렬)에 대해 설명부터 하려고 합니다.

3D를 표현하기전에
저희는 기존에 버텍스를(x,y,z,w) 다루었습니다.
( * 앞장까지는 x,y,z 만으로도 표현이 가능하였습니다. )

저희가 기억해야할 것은 w입니다.

• w = 1 이면 벡터공간에서의 점의 위치입니다. ( x, y, z, 1 )
• w = 0 이면 벡터공간에서의 방향입니다. ( x, y, z, 0 )

위의 내용은 무조건 기억하고 있어야합니다.

Matrix 이해

3D 그래픽스에서 4x4 행렬을 주로 사용하는데,
이들은 우리의 (x,y,z,w) 버텍스들을 변형하게 해줍니다. 이에 대한 공식은 아래와 같습니다.
행렬 x 버텍스 = 변형된 버텍스 ( * 순서가 동일해야합니다. )

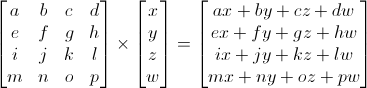
위의 공식은 GLSL에서는 아래와 같이 사용합니다.

1
2
3
4

mat4 Matrix;
vec4 Vector;

vec4 transformedVector = Matrix * Vector;

이처럼 저희는 변형된 버텍스 값을 사용하게되며,
앞서 말했던 (x,y,z,w) 벡터에 대해 설명하기 위해
이해하기 쉬운 평행이동 행렬에 대해 설명하겠습니다.

평행이동 행렬

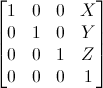
위의 행렬이 평행이동 행렬입니다.
X,Y,Z에 있는 것들이 자신의 위치에서 더하고자 하는 값입니다.

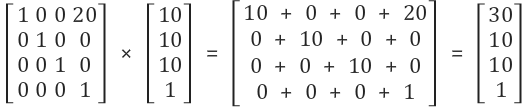
자신을 X 방향으로 20만큼 평행이동 시키면 위와 같이 계산을 하게되고,
결과는 벡터 ( 10, 10, 10, 1 )을 X 방향으로 20 이동시킨
( 30, 10, 10, 1 ) 벡터값을 얻게 됩니다.
(w = 1 일때 x 방향으로 이동하였으므로 위치가 변경되었습니다.)

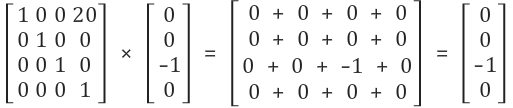
자신을 X 방향으로 20만큼 평행이동 시키면 위와 같이 계산을 하게되고,
결과는 벡터 ( 0, 0, -1, 0 )을 X 방향으로 20 이동시켰으나
변함이 없는 ( 0, 0, -1, 0 ) 벡터값을 얻게 됩니다.
(w = 0 일때 x 방향으로 이동하였으나 변화가 없습니다.)
이유는 바로 점은 이동하면 다른 좌표값을 갖는 점이 되지만 벡터는 이동한다고 방향이나 크기가 변하지 않기 때문입니다

단위 행렬

단위 행렬은 주 대각선이 1이고 나머지가 0인 행렬이고, 아무것도 하지않는 행렬입니다.

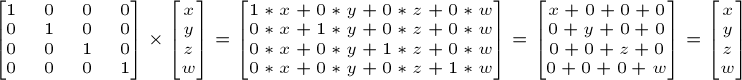
단위행렬에 벡터값(x, y, z, w)을 곱하면 벡터값 자신이 나오기 때문에 아무것도 하지 않습니다.

이를 이용하여 우리는 scale 매트릭스, translate 매트릭스, rotate 매트릭스등을 활용할 수 있습니다.
예를 들어 scale 매트릭스는 아래의 그림과 같습니다.

Scale 행렬

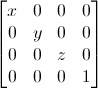
벡터값을 모든방향으로 2배 scale하려면

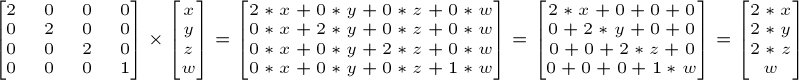
벡터값의 x,y,z가 아닌 scale 매트릭스의 x,y,z값을 2배로 주면 벡터값이 2배가 되고,
실제 코드에선 아래와 같이 사용됩니다.

1
2

mat4.scale(mvMatrix, [2.0, 2.0, 2.0]);
// 스캐일 매트릭스 사용법

!! 만약 scale, translate, rotate를 같이 사용할때는 꼭 순서를 지켜서 사용하여야 합니다.
순서는 translate -> rotate -> scale

위와 같이 단위 행렬, 평행이동 행렬, Scale 행렬 등 여러 행렬을 따로 구현 하는 것 보다는
이미 나와있는 기존의 라이브러리를 활용하는 것이 좋습니다.

우리는 gl-matrix라는 라이브러리를 사용하려고 하고,
해당 라이브러리의 주소는 http://glmatrix.net 입니다.

해당 페이지의 내용과 이미지의 출처는
https://webglfundamentals.org/ 입니다.