WebGL ( 7 - View )

이번장은 3D 도형을 구현하기전에 View 관점에 대해 설명하려고 합니다.
앞의 6장의 행렬과 관련된 내용입니다.

모델, 뷰, 프로젝션 Matrix ( MVP )

먼저 랜더링 간단한 랜더링 파이프라인은 이렇습니다.

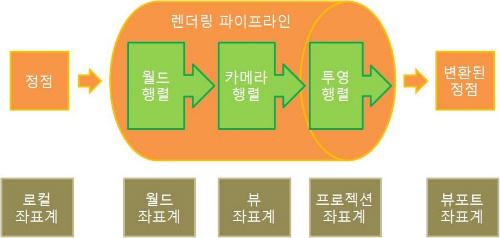
월드 -> 카메라 -> 투영행렬을 거쳐 3차원이 2차원으로 변환되는 과정입니다.
투영행렬이 끝난뒤에 클리핑과 뷰포트 변환이 있지만 여기서는 위와같이 투영 행렬까지만 설명합니다.

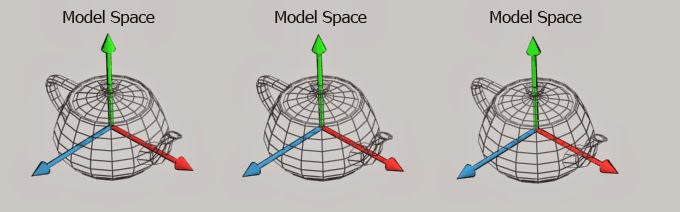
모델 Matrix는 모델좌표계에서 월드 좌표계로 변환해주는 행렬입니다.
( 6장에서 배운 translate, scale, rotate 변환이 모델 Matrix 입니다. )

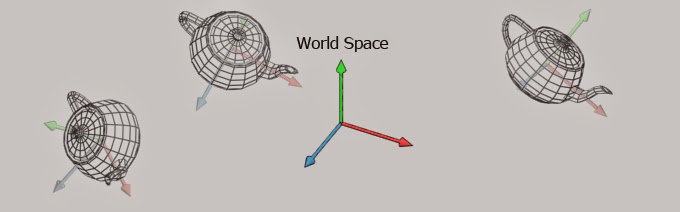
다음으로 월드 좌표계에서 카메라 좌표계로 변환해줘야 하는데
이때 뷰 Matrix를 사용합니다.
( 이 과정에서 카메라의 이동이라던지 카메라 위치 설정등이 이루어지고 lookAt 함수를 사용하게 됩니다. )

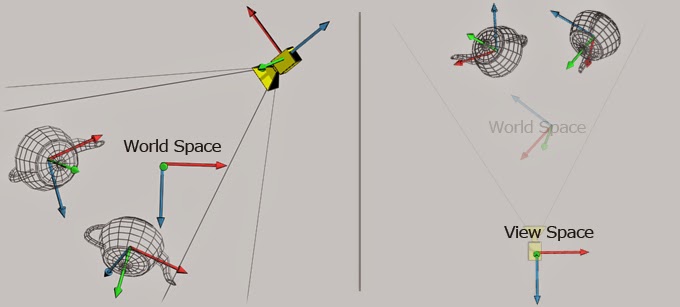
마지막으로 투영 변환 ( Projection Matrix )

월드 좌표계와 카메라 좌표계는 모두 3차원 좌표계입니다.
그러나 우리가 디스플레이로 확인하게 되는 랜더링 결과들은 모두 2차원의 화면입니다.
때문에 3차원 좌표계를 2차원 좌표계로 바꾸는 변환이 필요하다는 것을 알 수 있는데,
이때 투영 변환이 필요합니다.

투영 변환에는 perspective와 Orthographic가 있는데
우리는 perspective를 사용하도록 하겠습니다.

perspective

1
2
3
4
5
6
7
8

Ex)
mat4.perspective(view, canvas.width / canvas.height, 0.1, 2000.0, pMatrix);
// mat4.perspective 는 gl-matrix 라이브러리의 헬퍼 함수 
// (시야, 종횡비, 전방 및 후방 경계를 인자로 받는다.)
// 1. 시야 : 수직방향 시야각입니다.
// 2. 종횡비 : 화면 비 이고, 윈도우 크기에 의존합니다.
// 3. 근거리 잘라내기
// 4. 원거리 잘라내기

출처 : [webglfundamentals.org]

위의 변환까지 모두 완료가 되면 GLSL에서
Model, View, Projection 을 모두 곱해줘야합니다.
이때 행렬의 곱 순서는 꼭 mvp의 역순으로 곱해주어야 합니다.
( MVPmatrix = projection X view X model; )

1
2
3
4
5
6
7
8
9
10
11
12
13

<script id="shader-vs" type="x-shader/x-vertex">
    attribute vec3 aVertexPosition;
    attribute vec4 aVertexColor;

    uniform mat4 uMVMatrix;
    uniform mat4 uPMatrix;

    varying vec4 v_color;
    void main(void) {
      gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0);
      v_color = aVertexColor * 0.5 + 0.5;
    }
</script>

이번장은 여기서 마무리하고 다음장에서는 실제 3D 화면을 구현해 보도록 하겠습니다.

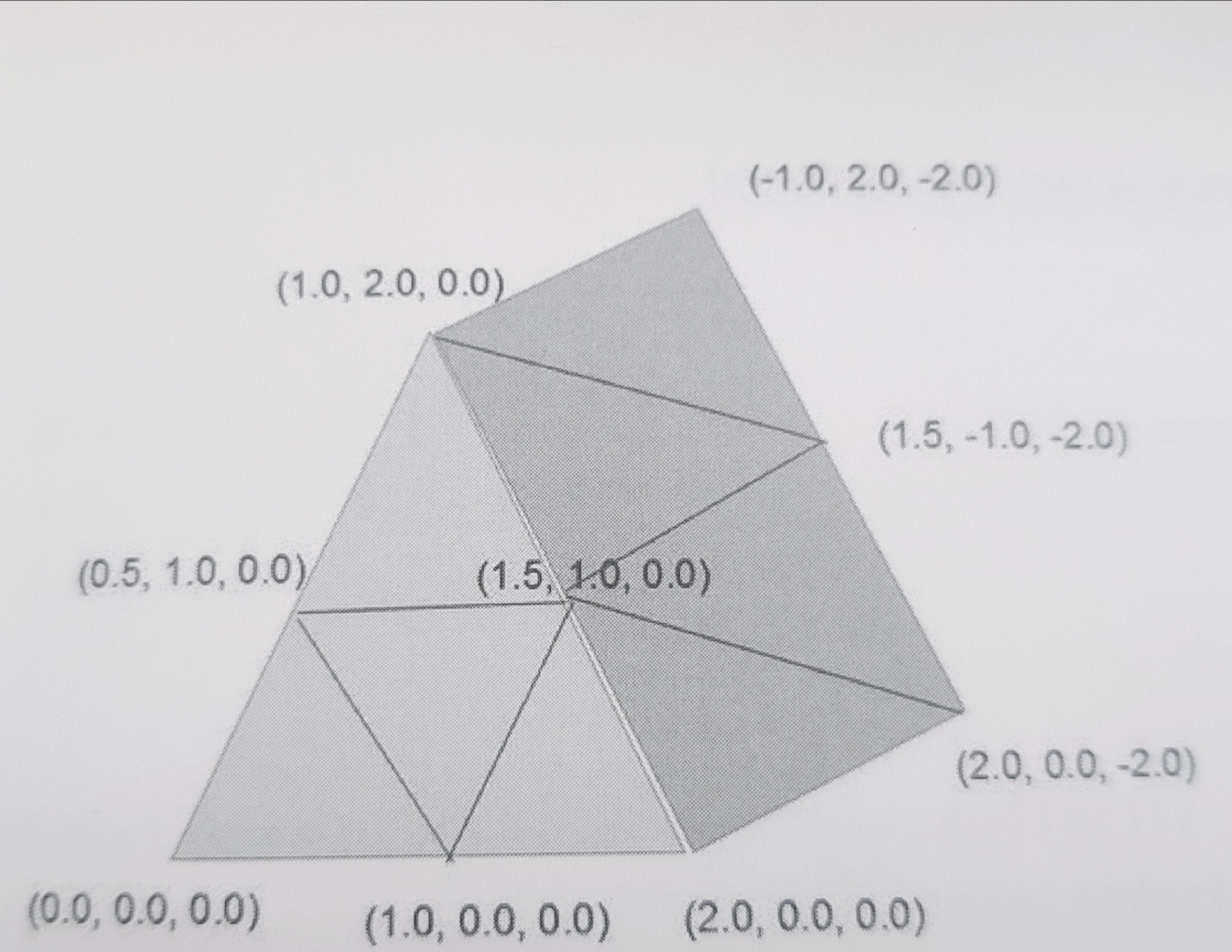
핵심 위치에 라벨을 붙임

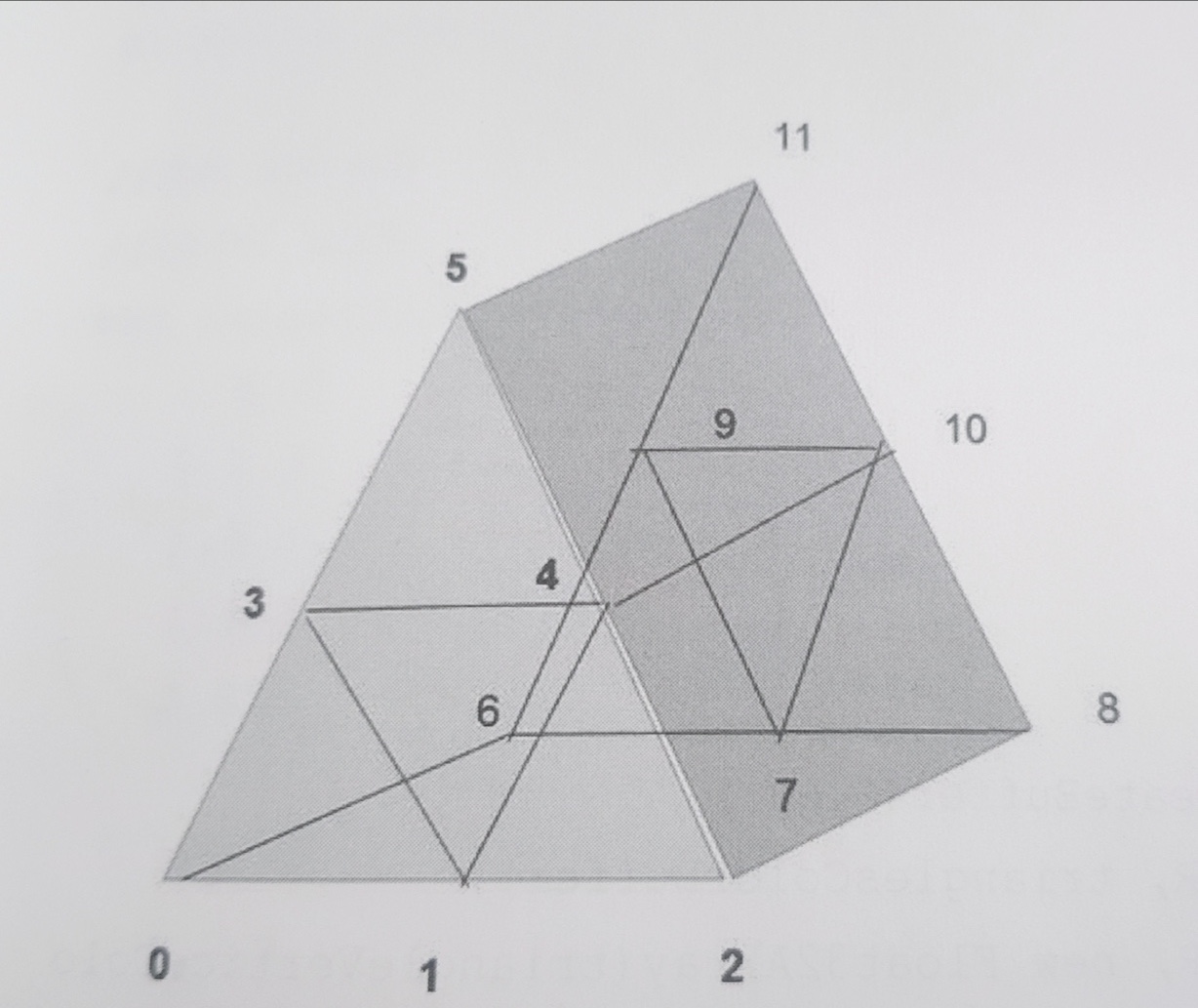
라벨을 붙인후 각 라벨에 인덱스 정점을 활용